Hello everyone!
In this post, we discuss whether [Dmg] or [CrtD] is the better weapon modifier for DPS runs. Besides answering this question for high end ISA runs, we also explain which parameter affect the performance of both modifier and under which conditions one is better than the other. [Dmg] outperforms [CrtD] for short high end ISA runs. We also recommend it, as it might be the more future-proof option considering future powercreep.
Approach
First, we want to show which parameters affect the [Dmg] and [CrtD] modifier and then explain which conditions have to be true that one modifier is better than the other. The following calculation applies to both ground and space combat.
For that, we take a look how the damage is calculated:
TotalDamage = (1+BaseDamage)*(1+BonusDamage)*FinalMultiplier
All base damage buffs are summed up and also all bonus damage buffs are summed up separately. Both sums are then multiplied with each other and with the product of all final multipliers. This means that base and bonus damage buffs are additive whereas final multiplier are multiplicative.
The [Dmg] modifier is a 1.03 final multiplier and [CrtD] is a 0.2 (20%) bonus damage buff applied on a critical hit. In the following, \(c_h\) refers to the critical hit chance, \(c_d\) the critical severity and \(d_s\), \(d_b\), \(d_f\) to base, bonus and final damage respectively. The average damage of a weapon including critical hits can be calculated as follows:
\(\mathcal{D}(c_h, c_d, d_s, d_b, d_f) = c_h((1+d_s)(1+d_b+c_d)*d_f) + (1-c_h)((1+d_s)(1+d_b)d_f) \tag{1}\)Using term 1, we can directly compare [Dmg] and [CrtD]. [Dmg] leads to a higher average damage than [CrtD] (=: [Dmg] \(\succ\) [CrtD] ) if and only if
where \(N\) is the number of modifiers to compare. Written out, the inequation looks as follows.
\(>\)
\(c_hd_f(1+d_s)(1+d_b+c_d+0.2N) + (1-c_h)(1+d_s)(1+d_b)d_f \)
which can be reduced by dividing both terms by \(d_f(1+d_s)\) (because \(d_f > 0\), \(d_s \geq 0\)) and applying further transformations (\(N > 0\), \(c_h > 0\)):
\( (1 + c_hc_d + d_b)/c_h > (0.2N) / (1.03^N -1) \tag{2}\)
Hence, [Dmg] is better than [CrtD] if the inequation 2 is evaluated as true. From this inequation, we can see that the critical chance, critical severity and bonus damage buffs determine whether [Dmg] increases the average damage more than [CrtD] or not. Base damage buffs and other final multipliers (besides the [Dmg] itself) are irrelevant for this comparison.
In the next step, we want to find an upper bound for [CrtD], at which it is safe to say that [Dmg] is superior. Since the performance of critical severity depends on the critical chance, the best case scenario for [CrtD] is a critical chance of 100%. This way we can find out, at which point [Dmg] is better than [CrtD] regardless of the critical chance. Setting the critical chance \(c_h\) to 100% for the inequation 2 yields:
The right side is a constant value \(f_N-1\) depending on the number of modifiers \(N\) to compare. Approximate values of this threshold for different \(N\in\{1,2,3,4\}\) are shown in the following table.
| N | 1 | 2 | 3 | 4 |
| \(f_N-1\) | 566.7% | 556.8% | 547% | 537.4% |
As an example, [Dmg]x4 leads to a higher average damage than [CrtD]x4 regardless of the critical chance, if the sum of the critical severity and bonus damage buffs are greater than ~537.4%.
There are cases, where a player cannot reach this threshold or is unable to maintain it. If the sum of bonus damage buffs and critical severity is less than this threshold, there exists a critical chance \(c_h < 100%\) where [CrtD] outperforms [Dmg]. To investigate this, we look into different scenarios.
Example Scenario: Minimal Buffs
In this scenario, we consider damage enhancements of a typical space DPS build that are permanent throughout a PvE. Higher critical severity and bonus damage favor [Dmg], so we need to know the minimum value for both that are always guaranteed.
Critical Severity:
- +50% Base
- +40% Skills
- +20% Advanced Targeting Systems
- +20% 4x SROs (at least, Vanguards might have more)
- +15% Colony Deflector (at 100% hull)
- +16% Tactical Fleet III
- +30% Endeavor
- +13.1% Tachyokinetic Converter
- +26.2% Bioneural Infusion Circuits
- +4% Fleet Boost
- +20% Epic weapon modifier
which is a total of 254.3% critical severity.
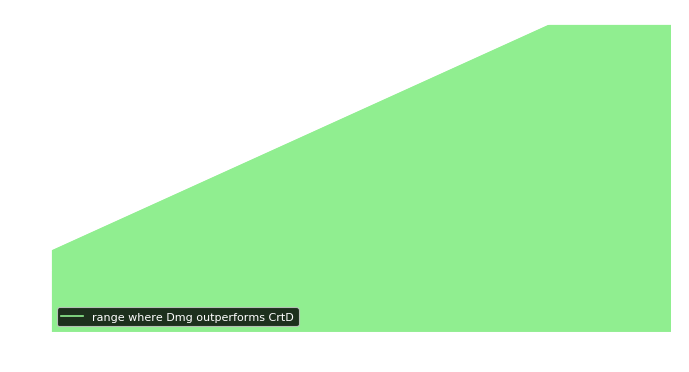
Figure 1 shows the relation between bonus damage and critical chance for the given critical severity of 254.3%. The green area represents the range in which [Dmg] is better than [CrtD] and the white area the range where [CrtD] is better than [Dmg]. This figure also shows that more bonus damage favors [Dmg]. In this case, a sum of 283.1% bonus damage buffs is required for [Dmg] \(\succ\) [CrtD] regardless of the critical chance.
Example Scenario: ISA
With the formula provided in the last section, [Dmg] \(\succ\) [CrtD] can be answered for any case by simply entering the critical chance, critical severity and bonus damage of a build. But since most bonus damage buffs come from active abilities, the available bonus damage buffs heavily depend on their usage and uptime. For example, high end ISA runs can be completed in under 30 seconds. Therefore short duration abilities like Go Down Fighting have a high uptime due to the shortness of such runs. We also know that the critical chance can exceed 80% in those runs. First, we look at permanent bonus damage increases:
- +40% Tactical Fleet III
- +7.5% Improved * Training
- +10% Fleet Coordinator
- +9.5% Controlled Countermeasurements
- +10% Emergency Power to Weapons I (up to 16.6 for rank 3)
Total: 77%
Most bonus damage increases come from abilities, so we have to count them in dynamically. To name some important buffs:
- +50% Go Down Fighting
- +20-50% Narrow Sensor Bands
- +40% Dynamic Power Redistributor
- +25% Domino (semi-permanent)
- +49.8% Alpha
- +30% Mixed Armaments Synergy I
For ~30s ISA runs, we can a assume a 100% uptime from the sides to the end for Alpha, Dynamic and Domino, which is another 114 bonus damage. Furthermore, Alpha provides an additional ~50% critical severity when it’s active. Scattering field and frenzy provide additional 67% bonus damage.
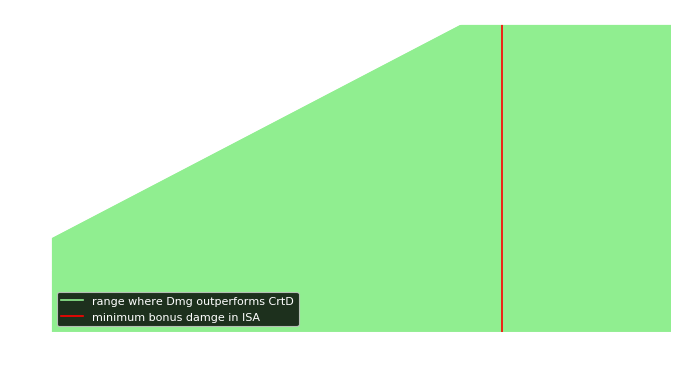
Figure 2 shows the same relation as Figure 1 for a high end ISA run with a critical severity of 304.1%. The red marker shows the minimum number of bonus damage for the entire ISA after the initial wave. The bonus damage is even higher when using additional buffs like Narrow Sensor Bands and Mixed Armaments Synergy. In this case, [Dmg] outperforms [CrtD] regardless of the critical chance.
Conclusions
- [Dmg] vs [CrtD] depends on the critical chance, critical severity and bonus damage. Base damage increases and other final multipliers (besides the [Dmg] itself) are irrelevant.
- For high end ISA runs, [Dmg] is better than [CrtD].
- [Dmg]x4 is better than [CrtD]x4 if the sum of bonus damage and critical severity is greater than 537.4% (or 547% for three mods, 556.8% for two mods and 566.7% for one mod).
~ Tirius@lordcruncher

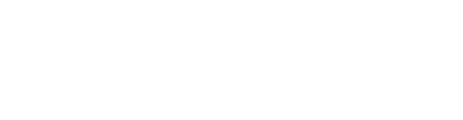






And here’s a simple spreadsheet: https://www.dropbox.com/s/rbf898735x58j2c/CrtD%20vs.%20Dmg.xlsx
Just enter your current CrtD and Bonus damage values and the number of mods to calculate.
Thank you for the effort you put into this Tirius. Very informative. 🙂
Not all buffs are constantly active, so in short fast runs avg dps might be higher using DMG and in longer runs avg dps might be higher using CrtD.
The graphs tells nothing about the avg amount of dps, it only shows how much Bonus damage is needed to have DMG>CtrD depending on the crt chance.
It’s correct that not all buffs are constantly active in an ISA. The purpose of the first scenario is to show all critical severity buffs that are constantly active on a player. Then you can read from the graph depending on your bonus damage buffs and critical chance which of both mods is better for your specific case. However, for short ISA runs (the ISA scenario only refers to high end ISA runs, not average runs) [Dmg] is the superior mod.
The DPS itself is not relevant to answer the question whether Dmg or CrtD leads to higher DPS. As shown in the approach section, only the relation between bonus damage, critical chance and critical severity (and the number of mods to compare) determines which mod is better.
Graph also does not say how much better the one modifier is compared to the other. Might be very litte difference % in practise, who knows.
Because that is not the point. 😉
The first figure shows the relation between crth and bonus damage affecting [Dmg] vs [CrtD]. The second figure shows that in fast ISA runs [CrtD] is inferior to [Dmg] because of the enormous bonus damage buffs.
But both are only examples how the math from the approach section can be applied. You can follow the same approach to compute the actual differences of both mods for your case.
I can’t understand how to use that dropbox calculator for the life of me.
So for a basic overall, as a tac you wanna go for [dmg] and as a eng you wanna go for [crtd] due to lesser damage buff sources? Or mixing [crtd] with [dmg] should be acceptable for both cases? Should the Advanced Fleet Weaponry mods be a formula for 100k-200k dps ranges? That being crtd+dmgx3?
I have all kinds of weapons with varied mods of crtd and dmg and I wanna have a general idea of the min-max trend on non-coordinated runs (mid-longer runs). [Crtd]x2 [dmg]x2? [Dmg]x4? [Crtd]x4?
It’s an excel file you’ll have to download. You can use it to play around with your bonus and crtd values to find the best mods for you. Base is just a default value. It’s more or less a simple tool to validate Tirius’ results.
In general any combination of CrtD and Dmg will work. If you want to be save, take two of each of them.
Short paragraph about sci and eng wouldve been nice
The excel has been downloaded. I don’t understand which fields to complete. Opened it with Libre’s excel and all of the values under the mods (4/4/4) are displayed as ####.
My actual calculation is on a 25-30% crth (non buffed – displayed in space) and 115% crtd ( non buffed – displayed in space)… Dmg or crtd?
I mention that these calculations are only for tac toons with A good day to die trait, so some constant +dmg cat2 and the APA are used pretty frequently.
For engineers and sci, haasinger, it’s simple. CrtD on everything. The amount of +dmg cat2 isn’t simply enough to turn that final +0.03xdmg multiplier into such a monster.
All you have to fill into the spreadsheet is your CrtD and Bonus value. Idk if it’s working in Libre office, probably not, bc. some cells have names. But it will work in Excel for cell phones.
About CrtD and Dmg for Scis/Engs
It really depends on your actual performance. I’d suggest you check your weapons CrtH in CLR (under Attack Abilities). My Eng’s crit chance in orbit is just 46.1%, in a PuG ISA it’s way above 70%. His CrtD in space is 184. With the epic mod, he’s at >200 before buffs. And now take Tirius’ list of bonus buffs. While Engs have no APA and GDF, they do have IER which is good for +50, so he’ll probably at 200 bonus. With those values Dmg and CrtD are almost equal. If he had less CrtH, Dmg would be the better choice.
Just resize the columms. LibreOffice will show you those #### when information in cells won’t fit 🙂
Nice work! Thanks for sharing this!
Is Tac Team iii preferred over attack patterns? I would be curious to see the difference in dps Gauntlet.
Tac Team 3 is +30 Energy Weapon Training which nets you +15 BaseDamage. Why waste a LtC Tac slot for this?
Past advice was to use APB or APO in the commander slot.
And this has changed recently?
Sorry, but I have a question. Is this saying that you shouldn’t worry about CrtD and CrtC? Or is it saying you shouldn’t trade DMG for either of the others?
I’m curious because I was wondering if it would be good to do a Crt build for Antiprotons, like it was years ago.
Thanks,
Razar.
Dmg and CrtD are both viable mods. If you are interested in maximizing the potential of your energy weapons, this post might help you understand which mods suits best to your build and situation.
You might also want to check out the ship building guides.
what’s mean (1+db+cd)? what is db? and why it’s same as cd?
The notation is explained in the paragraph above equation (1).
cdis your combined critical severity anddbyour combined bonus damage increases. They are not the same, but critical severity is applied in the same way as bonus damage increases on critical hits.I little bit modify last formula, but some rules on this site don’t give me rights to poste this, so I can say one thing of you have 200% of db and cd (both 400%) you should get more then 68% crit chance when CrtD better then Dmg, with 540% you need more then 101% crit chance
ch>(1.03^N-1)*(1+db)/(0.2*N-(1.03^N-1)*cd)when N=4, something like that